7. Trigonometric Substitutions

c. Completing Squares

The trig substitutions of the previous pages can be generalized still further. If the integrand contains a quadratic polynomial \(Ax^2+Bx+C\) then you can complete the square and rewrite the polynomial as either: \[ a^2(x-p)^2+b^2 \qquad \text{or} \qquad a^2(x-p)^2-b^2 \]

How do I complete the square?

To complete the square on the quantity \(Ax^2+Bx+C\), means to rewrite it in the form \(A[(x-p)^2+q]\) or \(\pm a^2(x-p)^2\pm b^2\). To find \(p\) and \(q\), we equate the expressions, expand and equate coefficients: \[\begin{aligned} Ax^2+Bx+C&=A[(x-p)^2+q]=A[x^2-2px+p^2+q] \\ &=Ax^2-2Apx+Ap^2+Aq \end{aligned}\] Consequently, \(B=-2Ap\) and \(C=Ap^2+Aq\). Solving gives: \[\begin{aligned} p&=-\,\dfrac{B}{2A} \\ q&=\dfrac{C}{A}-p^2=\dfrac{C}{A}-\dfrac{B^2}{4A^2} \end{aligned}\] At the end, we can write \(A=\pm a^2\) and \(Aq=\pm b^2\).

Don't memorize this formulas! Memorize the process.

In practice, we factor out the \(A\) and successively find \(p\) and then \(q\). For example: \[\begin{aligned} 4x^2-24x+20&=4(x^2-6x+5) \\ &=4(x^2-6x+9-4) \\ &=4[(x-3)^2-4] \\ &=2^2(x-3)^2-4^2 \end{aligned}\] To get the second and third lines, we looked at the coefficient of \(x\) which is \(-6=-2p\) to get \(p=3\). We square this to get the \(9\) and then identified \(q=-4\) to match the constant term \(5\).

In the former case, you can use a \(\tan\) substitution so that \(a(x-p)=b\tan\theta\). In the latter case, you can use a \(\sin\) or \(\sec\) substitution so that \(a(x-p)=b\sin\theta\) or \(a(x-p)=b\sec\theta\), depending on the size of \(|x-p|\). The \(\tan\) case is most common and most important:

Compute \(\displaystyle \int \dfrac{1}{x^2+6x+13}\,dx\).

We first complete the square: \[ x^2+6x+13=x^2+6x+9+4=(x+3)^2+4 \] Next we make the substitution \(x+3=2\tan\theta\). Then \(dx=2\sec^2\theta\,d\theta\) and: \[\begin{aligned} \int &\dfrac{1}{x^2+6x+13}\,dx =\int \dfrac{1}{(x+3)^2+4}\,dx \\ &=\int \dfrac{1}{4\tan^2\theta+4}2\sec^2\theta\,d\theta =\dfrac{1}{2}\int \dfrac{\sec^2\theta}{\sec^2\theta}\,d\theta \\ &=\dfrac{1}{2}\int 1\,d\theta =\dfrac{1}{2}\theta+C \end{aligned}\] To substitute back, we solve \(x+3=2\tan\theta\) for \(\theta=\arctan\dfrac{x+3}{2}\). Therefore \[ \int \dfrac{1}{x^2+6x+13}\,dx =\dfrac{1}{2}\arctan\dfrac{x+3}{2}+C \]

We check by differentiating. If \(f(x)=\dfrac{1}{2}\arctan\dfrac{x+3}{2}\), then: \[\begin{aligned} f'(x) &=\dfrac{1}{2}\dfrac{1}{1+\left(\dfrac{x+3}{2}\right)^2}\dfrac{1}{2} \\ &=\dfrac{1}{4+(x+3)^2}=\dfrac{1}{x^2+6x+13} \end{aligned}\] which is the integrand we started with.

Now it's your turn:

Compute \(\displaystyle \int \dfrac{1}{(4x-x^2)^{3/2}}\,dx\).

\[\begin{aligned} 4x-x^2&=-(x^2-4x) =-(x^2-4x+4-4) \\ &=-[(x-2)^2-4] =4-(x-2)^2 \end{aligned}\] Since this is inside of a \(\dfrac{3}{2}\) power, we let \(x-2=2\sin\theta\).

\(\displaystyle \int \dfrac{1}{(4x-x^2)^{3/2}}\,dx =\dfrac{1}{4}\dfrac{x-2}{\sqrt{4x-x^2}}+C\)

We first complete the square: \[\begin{aligned} 4x-x^2 &=-(x^2-4x)=-(x^2-4x+4-4) \\ &=-[(x-2)^2-4]=4-(x-2)^2 \end{aligned}\] Since this is inside of a \(\dfrac{3}{2}\) power, we let \(x-2=2\sin\theta\). Then \(dx=2\cos\theta\,d\theta\). The integral becomes: \[\begin{aligned} \int &\dfrac{1}{(4x-x^2)^{3/2}}\,dx =\int \dfrac{1}{[4-(x-2)^2]^{3/2}}\,dx \\ &=\int \dfrac{1}{[4-4\sin^2\theta]^{3/2}}2\cos\theta\,d\theta \\ &=\dfrac{1}{4}\int \dfrac{\cos\theta}{[1-\sin^2\theta]^{3/2}}\,d\theta =\dfrac{1}{4}\int \dfrac{\cos\theta}{\cos^3\theta}\,d\theta \\ &=\dfrac{1}{4}\int \sec^2\theta\,d\theta=\dfrac{1}{4}\tan\theta+C \end{aligned}\]

To substitute back, we know \(\sin\theta=\dfrac{x-2}{2}\). So we draw a right triangle with an angle \(\theta\) whose opposite side is \(x-2\) and whose hypotenuse is \(2\). These sides are chosen so that \(\sin\theta=\dfrac{x-2}{2}\). Then the adjacent side is \(\sqrt{4-(x-2)^2}\) and: \[ \tan\theta=\dfrac{x-2}{\sqrt{4-(x-2)^2}}=\dfrac{x-2}{\sqrt{4x-x^2}} \]

trisqsin12

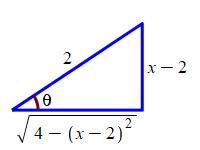
So the integral becomes: \[ \int \dfrac{1}{(4x-x^2)^{3/2}}\,dx =\dfrac{1}{4}\dfrac{x-2}{\sqrt{4x-x^2}}+C \]

We check by differentiating. If \(f(x)=\dfrac{1}{4}\dfrac{x-2}{\sqrt{4x-x^2}}\), then \[\begin{aligned} f'(x) &=\dfrac{1}{4}\dfrac{\sqrt{4x-x^2}(1)-(x-2)\dfrac{4-2x}{2\sqrt{4x-x^2}}}{4x-x^2} \\ &=\dfrac{1}{4}\dfrac{(4x-x^2)-(x-2)(2-x)}{(4x-x^2)^{3/2}} \\ &=\dfrac{1}{4}\dfrac{(4x-x^2)-(-x^2+4x-4)}{(4x-x^2)^{3/2}} \\ &=\dfrac{1}{(4x-x^2)^{3/2}} \end{aligned}\] which is the integrand we started with.